Tangent and Normal of a Circle

The equation of circle such that the length of the tangent to it from the points $(1,0),\left(2,0\right)$ and $\left(3,2\right)$ are $1,$ $\sqrt{7}\text{,} \sqrt{2}$ respectively, is

Let ABCD be a quadrilateral with area 18, with sides AB parallel to the side CD and AB = 2CD. Let AD be perpendicular to AB and CD. If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is 

Consider a circle S with centre at the origin and radius $4$. Four circles $A, B, C$ and $D$ each with radius unity and centres $\left(-3,0\right), \left(-1,0\right), \left(1,0\right)$ and $\left(3,0\right)$ respectively are drawn. $A$ chord $PQ$ of the circle $S$ touches the circle $B$ and passes through the centre of the circle $C$. If the length of this chord can be expresses as $\sqrt{x}$, find $x$.

The lines $3x-4y+4=0$ and $6x-8y-7=0$ are tangents to the same circle. The radius of this circle is

Consider the circle $C$ that passes through the points $\left(1,0\right)$ and $\left(0,1\right)$ having the smallest area. Then, the equation of the tangent to the circle $C$ at $\left(0,1\right)$ is

Find the slope of the focal chords of the parabola $y^2=32x$, which are tangents to the circle $x^2+y^2=4$ 

If the lines $3x–4y+4=0 \& 6x–8y–7=0$ are tangents to a circle, then find the radius of the circle.

Find the parametric coordinates of the circle $x^2+y^2=4$ and also, find the equation of the tangent using the parametric coordinates.

The equation of normal which is at a maximum distance from$\left(-1, -1\right)$ and drawn to the circle ${\left(x-1\right)}^2+{\left(y-2\right)}^2=4$ is

The tangent at $A(-1,2)$ on the circle $x^2+y^2-4x-8y+7=0$ touches the circle $x^2+y^2+4x+6y=0$ at $B$. Then, a point of trisection of $AB$ is

Centres of two circles having radius $2$ and $1$ units respectively are $5$ units apart. The area of the quadrilateral formed by joining the points of contact of external tangents drawn to two circles is equal to (in sq. units)

For next two question please follow the same

A tangent line is drawn to a circle with unit radius at the point $\mathrm{A}$ and a segment $\mathrm{AB}$ is laid off whose length is equal to that of the arc $\mathrm{AC}$, a straight line $\mathrm{BC}$ is drawn to intersect the extension of the diameter $\mathrm{AO}$ at the point $\mathrm{P}$.

​​​​​​​

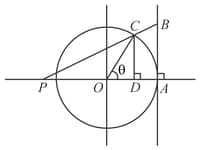
The area of the trapezoid $\mathrm{ABCD}$ is 

Let $C$ be the circle concentric with the circle, $2x^2+2y^2-6x-10y=183$ and having area ${\left(\frac{1}{10}\right)}^{\mathrm{th}}$ of the area of this circle. Then a tangent to $\mathrm{C},$ parallel to the line, $3 x+y=0$ makes an intercept on the $y$-axis, which is equal to

From a fixed point $A$ on the circumference of a circle of radius $r$, $AY$ is the perpendicular on the tangent at $P$ of the circle, then maximum area of the triangle $APY$ is equal to 

If $y=f\left(x\right)=ax+b$ is a tangent to circle $x^2+y^2+2x+2y-2=0$, then ${\left(a+b\right)}^2+2\left(a-b\right)\left(a+b+1\right)$ $=$______

Let's take a circle $x^2+y^2-2x-4y-20=0$ with centre $A$, what will be the area of quadrilateral $ABCD$, if the tangents to the circle at points $B\left(1,7\right)$ and $C\left(4,-2\right)$ meet at a point $D$?

A circle has a diameter having the coordinates as $\left(3,7\right)$ and $\left(9,1\right)$, also this circle touches the line $x+y=4$, find the coordinates of point of contact :

Find the equation of the tangent to circle $5x^2+5y^2=1$, parallel to line $3x+4y=1$.

Consider a circle in $xy$-plane with diameter $1$ , passing through the origin $O$ and through the point A given as $\left(1,0\right).$ $\mathrm{B}$ is any point on the circle. Let $C$ be the point of intersection of line $OB$ with the vertical line through $A$. If $M$ is the point on the line $OBC$ such that $OM$ and $BC$ are of equal length, then the locus of point $M$ as $B$ varies is given by the equation